Approximation of analytic functions by generalized shifts of the Lerch zeta-function
Abstract
In the paper, we approximate analytic functions by generalized shifts ![]() of the Lerch zeta-function, where g is a certain increasing to
of the Lerch zeta-function, where g is a certain increasing to ![]() real function having a monotonic derivative. We prove that, for arbitrary parameters λ and α, there exists a closed set
real function having a monotonic derivative. We prove that, for arbitrary parameters λ and α, there exists a closed set 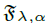 of analytic functions defined in the strip 1/2 < σ < 1 which functions are approximated by the above shifts. If the set of logarithms
of analytic functions defined in the strip 1/2 < σ < 1 which functions are approximated by the above shifts. If the set of logarithms ![]() is linearly independent over the field of rational numbers, then the set
is linearly independent over the field of rational numbers, then the set 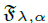 coincides with the set of all analytic functions in that strip.
coincides with the set of all analytic functions in that strip.
Keyword : Lerch zeta-function, Mergelyan theorem, space of analytic functions, universality, weak convergence

This work is licensed under a Creative Commons Attribution 4.0 International License.
References
T.M. Apostol. Addendum to “On the Lerch zeta function”. Pacific Journal of Mathematics, 2(1):10, 1952. https://doi.org/10.2140/pjm.1952.2.10
B. Bagchi. The Statistical Behaviour and Universality Properties of the Riemann Zeta-Function and Other Allied Dirichlet Series. PhD Thesis, Indian Statistical Institute, Calcutta, 1981.
B.C. Berndt. Two new proofs of Lerch’s functional equation. Proceedings of the American Mathematical Society, 32(2):403–408, 1972. https://doi.org/10.1090/S0002-9939-1972-0297721-3
P. Billingsley. Convergence of Probability Measures. Willey, New York, 1968.
R. Garunkštis, A. Laurinčikas and R. Macaitienė. Zeros of the Riemann zeta-function and its universality. Acta Arithmetica, 181(2):127–142, 2017. https://doi.org/10.4064/aa8583-5-2017
S.M. Gonek. Analytic Properties of Zeta and L-Functions. PhD Thesis, University of Michigan, 1979.
M. Jasas, A. Laurinčikas, M. Stoncelis and D. Šiaučiūnas. Discrete universality of absolutely convergent Dirichlet series. Mathematical Modelling and Analysis, 27(1):78–87, 2022. https://doi.org/10.3846/mma.2022.15069
A.A. Karatsuba and S.M. Voronin. The Riemann Zeta-Function. Walter de Gruyter, Berlin, 1992. https://doi.org//10.1515/9783110886146
M. Korolev and A. Laurinčikas. A new application of the Gram points. Aequationes mathematicae, 93(5):859–873, 2019. https://doi.org/10.1007/s00010-019-00647-8
M. Korolev and A. Laurinčikas. A new application of the Gram points. II. Aequationes mathematicae, 94(6):1171–1187, 2020. https://doi.org/10.1007/s00010-020-00731-4
A. Laurinčikas. Limit Theorems for the Riemann Zeta-Function. Kluwer, Dordrecht, 1996. https://doi.org/10.1007/978-94-017-2091-5
A. Laurinčikas. The universality of the Lerch zeta-function. Lithuanian Mathematical Journal, 37(3):275–280, 1997. https://doi.org/10.1007/978-94-017-2091-5
A. Laurinčikas. On discrete universality of the Hurwitz zeta-function. Results in Mathematics, 72(1):907–917, 2017. https://doi.org/10.1007/s00025-017-0702-8
A. Laurinčikas. “Almost” universality of the Lerch zeta-function. Mathematical Communications, 24(1):107–118, 2019.
A. Laurinčikas. Discrete universality of the Riemann zeta-function and uniform distribution modulo 1. St. Petersburg Mathematical Journal, 30(1):103–110, 2019. https://doi.org/10.1090/spmj/1532
A. Laurinčikas and R. Garunkštis. The Lerch Zeta-Function. Kluwer Academic Publishers, Dordrecht, Boston, London, 2002.
A. Laurinˇcikas, R. Macaitiene˙, D. Mochov and D. Siauˇciu¯nas. Universality of theˇ periodic Hurwitz zeta-function with rational parameter. Siberian Mathematical Journal, 59(5):894–900, 2018. https://doi.org/10.1134/S0037446618050130
A. Laurinčikas, R. Macaitienė and D. Šiaučiūnas. A generalization of the Voronin theorem. Lithuanian Mathematical Journal, 59(2):156–168, 2019. https://doi.org/10.1007/s10986-019-09418-z
A. Laurinčikas, R. Macaitienė and D. Šiaučiūnas. Universality of an absolutely convergent Dirichlet series with modified shifts. Turkish Journal of Mathematics, 46(6):2440–2449, 2022. https://doi.org/10.55730/1300-0098.3279
A. Laurinčikas, T. Mikalauskaitė and D. Šiaučiūnas. Joint approximation of analytic functions by shifts of Lerch zeta-functions. Mathematics, 11(3), 2023. https://doi.org/10.3390/math11030752
A. Laurinčikas, D. Šiaučiūnas and M. Tekorė. Joint universality of periodic zeta-functions with multiplicative coefficients. II. Nonlinear Analysis: Modelling and Control, 26(3):550–564, 2021. https://doi.org/0.15388/namc.2021.26.23934
A. Laurinčikas and M. Tekorė. Joint universality of periodic zeta-functions with multiplicative coefficients. Nonlinear Analysis: Modelling and Control, 25(5):860–883, 2020. https://doi.org/10.15388/namc.2020.25.19278
M. Lerch. Note sur la fonction K(w,x,s) = Pn⩾0 exp{2πinx}(n + w)−s. Acta Mathematica, 11:19–24, 1887. https://doi.org/10.1007/BF02612318
K. Matsumoto. A survey on the theory of universality for zeta and L-functions. In M. Kaneko, S. Kanemitsu and J. Liu(Eds.), Number Theory: Plowing and Starring Through High Wawe Forms, Proc. 7th China-Japan Semin. (Fukuoka 2013), volume 11 of Number Theory and Appl., pp. 95–144, New Jersey, London, Singapore, Beijing, Shanghai, Hong Kong, Taipei, Chennai, 2015. World Scientific Publishing Co.
S.N. Mergelyan. Uniform approximations to functions of complex variable. Usp. Mat. Nauk., 7(2):31–122, 1952. Available on Internet: http://wonder.cdc.gov/ucd-icd10.html (in Russian)
M. Mikolás. New proof and extension of the functional equality of Lerch’s zetafunction. Annales Universitatis Scientiarum Budapestinensis de Rolando Eötvös Nominatae. Sectio Mathematica, 14:111–116, 1971.
F. Oberhettinger. Note on the Lerch zeta function. Pacific Journal of Mathematics, 6(1):117–120, 1956. https://doi.org/10.2140/pjm.1956.6.117
Ł. Pańkowski. Joint universality for dependent L-functions. The Ramanujan Journal, 45(1):181–195, 2018. https://doi.org/10.1007/s11139-017-9886-5
D. Šiaučiūnas and M. Tekorė. Gram points in the universality of the Dirichlet series with periodic coefficients. Mathematics, 11(22):article no. 4615, 2023. https://doi.org/10.3390/math11224615
J. Steuding. Value-Distribution of L-Functions. Lecture Notes Math. vol. 1877, Springer, Berlin, Heidelberg, 2007. https://doi.org/10.1007/978-3-540-44822-8
S.M. Voronin. Theorem on the “universality” of the Riemann zeta-function. Izvestiya Rossiiskoi Akademii Nauk. Seriya Matematicheskaya, 39(3):475–486, 1975. https://doi.org/10.1070/IM1975v009n03ABEH001485 (in Russian)
